Heat Source Modeling and Study on the Effect of Thickness on Residual Stress Distribution in Electron Beam Welding

Leila Rajabi; Majid Ghoreishi

doi:10.5781/JWJ.2017.35.1.49

Abstract

In this study, the volumetric heat source in electron beam welding (EBW) is modeled through finite element method taking advantage of ABAQUS software package. Since this welding method is being applied in plates with different thicknesses and also considering that residual stresses reduce the strength of these weldments, the effect of thickness in the distribution and magnitude of residual stresses after welding is studied. Regarding the vast application of Inconel 706 super-alloy in aerospace industries, this material was selected in the current research. In order to validate the finite element model, the obtained results were compared to those of other researchers in this area, and good agreement was observed. The simulation results revealed that increase in the plate thickness leads to increase in the residual stresses. In addition heat treatment in the base metal (before welding) increases the residual stresses significantly.

Key words: Electron-beam welding, Finite element modeling, Inconel 706, Residual stresses, Thickness

1. Introduction

Nickel-based super-alloys comprise a considerable proportion of researches in aerospace industries. The corrosion and creep resistance properties associated with these alloys has made them fundamental materials for motor parts in hot sections such as turbine disks and fins. In such applications, assembly of various parts taking advantage of welding constitutes a significant stage in design and manufacture of these products. Therefore, weldability study of such materials is of foremost importance. Owing to some properties attributed to these materials, welding technologies with high power densities, especially electron beam welding (EBW), are applied. As a matter of fact, this welding technology entails the smallest fusion zone and heat effected zone, and this fact leads to reduction of distortions and residual stresses. Nevertheless, presence of residual stresses in critical parts can decrease their life and strength.

Owing to the critical applications of electron beam welding, many researches in the past years have focused on this welding process. In 2001, Koleva^¹⁾ conducted a statistical mult-response study on electron beam welding of stainless steel samples in order to optimize the process. Zhu et al.^²⁾ in 2002 studied the effect of temperature-dependent material properties on weldments through 3D nonlinear analysis of welding taking advantage of finite element method. In 2003, Couedel et al.^³⁾ modeled a moving heat source through 2D finite element modeling. Ferro et al^⁴⁾ in 2004 carried out a numerical and experimental research on plates made from the nickel-based super-alloy of Inconel 706 in order to study the effect of electron beam welding parameters on geometrical and microstructural properties. In the same year, Ram et al^⁵⁾ presented design of experiments and parameter optimization in electron beam welding making use of variance analysis. In 2005, Ho^⁶⁾ analytically studied the effects of conical specifications of the electron beam on the fusion zone. The same author in 2007 in another paper^⁷⁾ proposed an analytical 3D solution for prediction of temperatures in the welding pool of electron beam welding. One year later, Zhao et al.^⁸⁾ studied residual stress and distortion reductions in electron beam welding taking advantage of multiple beams technique, and investigated the topic through finite element analysis and experimental studies. In the same year Qi et al.^⁹⁾ took advantage of high energy density, high absorption rate and vacuum environment of electron beam technology in Electron beam selective melting316 stainless steel powders. In 2009, Luo et al.^¹⁰⁾ simulated the thermal effect of electron beam welding in a magnesium alloy through 3D modeling of the heat source in vacuum. Liu et al.^¹¹⁾ in 2011 studied variation of welding residual stresses after material removal from a 50 mm thick plate of a titanium alloy welded through electron beam welding. In a recent study in 2011, Jha et al.^¹²⁾ conducted different experiments on 304 stainless steel plates in order to control welding outputs in terms of yield strength and ultimate tensile strength through monitoring input parameters namely accelerating voltage, beam current, and welding speed. They took advantage of neural networks in their optimization.

In this study, Finite element simulation is utilized to model the welding process and predict the consequent residual stresses. Here, ABAQUS software package was employed to conduct finite element modeling, and the results obtained were compared to those in^⁴⁾, in order to validate the model. The agreement observed between the results provided confidence in the validity of the model.

2. Heat Source Model For EBW

Fig. 1 illustrates the combined heat source model applied in this study. The effect of heat diffusion associated with the keyhole is simulated through a three-dimensional conical heat source model. In other words, the metal vapor with a temperature higher than boiling point with local thermodynamic equilibrium bears the same properties as a surface heat source. A Gaussian surface heat source model is applied to simulate the surface thermal effects.

Fig. 1

The combined heat source model

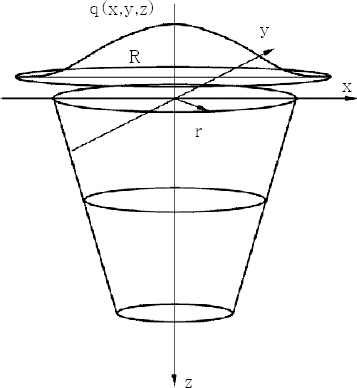
The distribution of the heat flux associated with the surface source is as below:

(1)

q(x,y)=q0×exp[−r2R2]

(2)

q0 = ηQ0V1

(3)

Q0 = V.I

where V denotes voltage, I is amperage, V₁ denotes the volume of the spherical heat source, and R represents the effective radius of the electron beam. According to the rotating body property, x²+y²=r², where r is the radial distance of each point in the heat source from the center.

When the welding heat source moves on, the inlet heat flux alters in the different positions throughout the welding path. Thus, the moving coordinates and the stationary ones are related as:

(4)

u = y +υ(τ−t)

where t is the welding period, and υ is the welding speed. After transformation between stationary and moving coordinates, Equation (1) is modified into Equation (5):

(5)

q(x,y) = q0 ×exp[3[x2+(y+υ(τ−t))2R2]

where x²+u²=r².

The distribution of the heat flux associated with the conical heat source is according to the following:

(6)

q(x,y,z) = q0×exp[−r2r02]

(7)

r0 = Re−(Re−Ri)⋅(Ze−Z)⋅(Ze−Zi)

where V is the voltage, I represents the amperage, and V₂ denotes the volume of the conical heat source. The other parameters are provided in Table 1.

Table 1

Simulation parameters

Heat source	Spherical	Conical
q₀(W/mm²)	215	-
R1(mm)	0.9	-
R2(mm)	1.3	-
Ri(mm)	-	0.47
Re(mm)	-	0.49
Zi(mm)	-	2.7
Ze(mm)	-	8.8

The value of η (heat input efficiency) in both heat sources has been considered as 0.8.

3. Finite element simulation of ebw

Numerical modeling of welding processes through finite element method is carried out through one the following two approaches. In the first approach designated as sequentially coupled analysis, the thermal results are first extracted through solution of a pure heat transfer problem, and the thermal history of nodes and elements are applied as the input to the next phase which is the mechanical analysis in which the resulting stresses are calculated based upon the thermal history of weldments through incorporation of thermal expansion coefficient. In the other approach, fully coupled analysis, the thermal and mechanical fields are studied at the same time through solution of all the thermal and mechanical equations in their initial coupled format. The latter approach is more complicated in comparison with the sequentially coupled analysis, and thus, it is justified when the nonlinearity of equations are too high to be treated in an uncoupled manner^¹³⁾.

In the present study, in view of the fact that the heat produced through elasto-viscoplastic straining is negligible compared to the heat input, the sequentially coupled analysis is selected. In other words, the analysis is carried out throughout uncoupled thermal and mechanical analyses, in which the thermal history of the weldments is computed independently with the results introduced to the mechanical analysis for calculation of the residual stresses.

3.1 Welding parameters

As previously discussed, the experimental results of^⁴⁾ have been utilized in validation of the finite element model. The geometry and dimensions of the plates in this experimental work are depicted in Fig. 2.

Fig. 2

Geometry and dimensions of the simulated plates

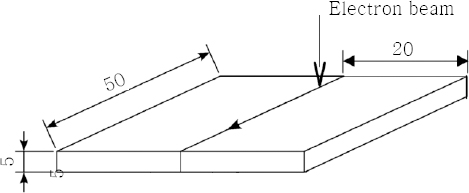
In the experimental work conducted in^⁴⁾, V = 150kv, I=10mA and v = 10mm/s have been considered, and the same parameters were included in the present work.

3.2 Thermal analysis of ebw process

A 3D finite element model comprised of 82077 nodes and 66500 elements of type DC3D8 (having thermal degrees of freedom) was created to solve the heat transfer problem, as illustrated in Fig. 3. As observed, the welding zone bears a finer mesh owing to the higher temperature gradient, while the regions farther from the weld line include a coarser mesh to decrease the computational cost. Regarding the symmetry, one half of the weldments is modeled for further reduce the computational cost.

Fig. 3

The finite element model applied

In order to simulate the heat source, a USER-SUBROUTINE encompassing two conical and Gaussian heat sources was provided utilizing the aforementioned equations. These codes are written making use of FORTRAN programming language^¹⁴⁾.

The thermo-physical material properties incorporated in the research are presented in Table 2.

Table 2

Thermo-physical properties of Inconel 706^¹⁵⁾

Temperature (°C)	Conductivity (W/m.°C)	Specific heat (J/kg.°C)
0	12.5	444
100	14	461
150	14.8	473
200	15.9	490
250	16.7	502
300	17.6	515
350	18.5	528
400	19.2	536
450	19.9	553
500	20.6	565
550	21.3	582
600	22.1	595
650	-	607
700	-	620
1000	-	650
1100	-	680
1400	-	720

3.3 Mechanical analysis of ebw process

For mechanical analysis, the same finite element model presented in the thermal analysis is applied, and as discussed before, the thermal history obtained in the thermal analysis is applied as the load, and solution of the fundamental equations of elasticity and thermo-elasticity along with incorporation of the mechanical properties attributed to the material (Table 3) lead to the desired results, i.e. residual stresses.

Table 3

Mechanical properties of Inconel 706^¹⁵⁾

Temperature (°C)	Yield Stress (MPa)	Thermal Expansion Coefficient (°C)	Young’s Modulus (GPa)	Poisson’s Ratio
0	383	1/30×10^-5	204	0.382
100	369	1/41×10^-5	193	0.389
200	352	1/45×10^-5	187	0.392
300	339	1/50×10^-5	181	0.403
400	336	1/54×10^-5	176	0.404
600	316	1/60×10^-5	165	0.395
700	272	1/64×10^-5	155	0.415
1000	52	1/78×10^-5	72	0.420
1100	45	1/90×10^-5	30	0.432
1400	20	2×10^-5	25	0.440

4. Results and discussion

In this section, the results associated with finite element modeling of EBW process are provided. First, the finite element code is validated through comparison with the results provided in^⁴⁾. After enough confidence is reached about validity of the model, further predictions and investigations about the effect of plate thickness on the residual stresses are made.

4.1 Validation of the model

Fig. 4 displays the stress contours during electron beam welding of the plates.

Fig. 4

Stress contours during EBW process simulation

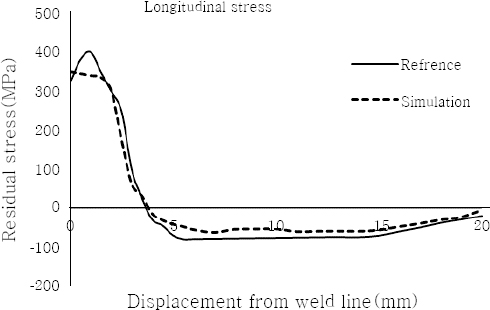
Figs. 5 and 6 compare the transverse and longitudinal stresses obtained through the present study and those of^⁴⁾. As observed, good agreement exists between the results, which reveals the validity of the procedure.

Fig. 5

Comparison of simulation results and those of^⁴⁾ (transverse stresses)

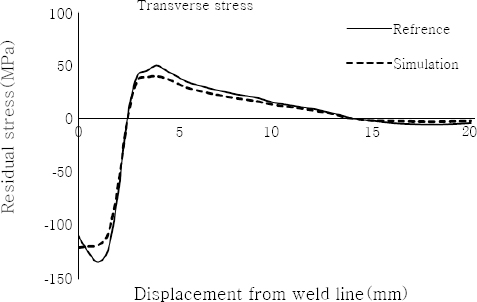
Fig. 6

Comparison of simulation results and those of^⁴⁾ (longitudinal stresses)

4.2 pre-heat treatment

Inconel 706 is a wrought Ni-Fe base super alloy which is widely used in the gas turbine Industry. e.g. for disc applications, because of its balanced manufacturability and elevated temperature strength. Heat treatment is an indispensable step in the manufacture of Inconel alloy products. However, apart from the desired effects, the heat treatment process can be accompanied by unwanted effects such as component distortion, increased residual which can lead to fatigue failure. Therefore, success or failure of heat treatment not only affects manufacturing costs but also determines product quality and reliability. Heat treatment must therefore be taken into account during development and design, and it has to be controlled in the manufacturing process and considered in welding processes.

Ultimate strength and 0.2% offset yield strength of Inconel 706 weldments at room temperature, 1200 F (649 C), and 1400 F (760 C) was above 90% that of base metal and in most cases exceeded the minimum level specified by AMS 5596 and MIL-Hdbk-5B for base metal^¹⁶⁾.

4.3 Pre-heat treatment procedures]

Solution anneal at 1700 to 1850 F and air cool. Then there are 2 follow on heat treatments: For optimum creep/rupture properties follow the solution anneal with 1550 F for 3 hours, air cool -- then 1325 F precipitation treatment for 8 hours followed by cooling rate of 100 F per hour down to 1150 F. Hold at 1150 F for 8 hours and air cool. For optimum tensile strength follow the solution anneal with 1350 F precipitation heat treatment for 8 hours, followed by cooling rate of 100 F per hour down to 1150 F. Hold at 1150 F for 8 hours and air cool. This treatment eliminates the 1550 F thermal treatment^¹⁷⁾.

4.4 Effect of base metal heat treatment prior to welding on residual stresses

After enough confidence is found, it is available to study the effect of heat treatment on the distribution and magnitude of the residual stresses. The results presented in Figs. 5 and 6 were obtained making use of heat treated material properties, as used in^⁴⁾. An important question to be answered is how heat treatment of initial materials affects the final residual stresses. In other words, does heat treatment which allows for much higher strength for the material include any drawbacks? Heat treatment imposes dramatic changes in the plastic properties of the material. In this regard, the mechanical properties of non-heat treated Inconel 706 were incorporated and the residual stresses were calculated and compared to the initial results. The results are presented in Figs. 7 and 8 for longitudinal and transverse stresses, respectively.

Fig. 7

Effect of heat treatment on longitudinal stresses

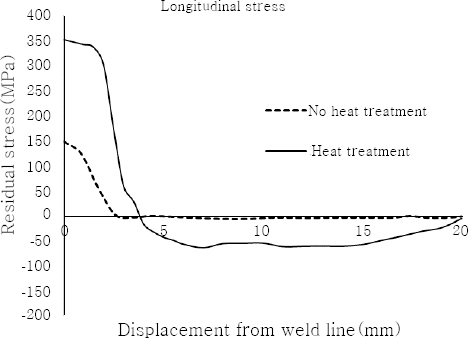
Fig. 8

Effect of heat treatment on transverse stresses

As presented, heat treatment of the material imposes vast changes in the residual stresses, which needs to be taken into consideration. This occurs as a consequence of the fact that the maximum residual stress tends to equal the yield strength. Therefore, the increase in residual stresses as a result of heat treatment leads to a dramatic increase in the residual stresses which imposes practical limitations.

4.5 Effect of plate thickness on residual stresses

After studying the effect of heat treatment, plate thickness effect is another parameter studied in this work. In this regard, thicknesses of 10 mm and 2.5 mm were considered and compared to the original thickness of 5 mm (twice and half the original thickness). Figs. 9 and 10 illustrate this comparison.

Reflection on the presented results reveals that increase in the thickness of the plates leads to rise in the maximum residual stresses, which can be justified through consideration of the stricter internal constraints within the material that occurs with increase in the material thickness. This is a significant result as EBW is especially applied on plates with high thickness, and this fact must be considered.

5. Conclusions

In this study, finite element simulation of electron beam welding was studied in order to investigate the effect of heat treatment (on base metal before welding) and plate thickness on the distribution and magnitude of welding residual stresses. The results obtained in^⁴⁾ were utilized to validate the finite element model. Through fulfillment of this study, the following conclusions were drawn:

1) Comparison of the obtained finite element results with those of a previous study revealed the validity of the conducted procedure.

2) Heat treatment of the base metal (before welding) can significantly increase the strength of the material. However, this increase in the yield stress also increases the residual stresses significantly.

3) Increasing the plate thickness increases the residual stresses within the material which must be considered; as the high efficiency of EBW in welding of thick plates with the least number of passes might lead to ignorance of the very fact that high residual stresses are a significant limitation.