전산유체역학을 활용한 마찰교반용접의 해석적 접근에서 표면추적을 위한 알고리즘 연구
A study on an Interface Tracking Algorithm in Friction Stir Welding based on Computational Fluid Dynamics Analysis
Article information
Abstract
Friction stir welding(FSW) was studied using commercial tool, FLOW-3D. The purpose of this study is to suggest a method to apply frictional heat in Computational fluid dynamics(CFD) analysis. Cylindrical tool shape was used, and the interface cells between tool surface and workpiece were tracked by its geometrical relations in order to consider the frictional heat in FSW. After tracking the interface cells, average area concept was used to calculate the frictional heat, which is related to interface area. Also three-dimensional heat source and visco-plastic flow were modeled. The frictional heat generation rate calculated numerically from the suggested algorithm was validated with the analytical solution. The numerical solution was well matched with the analytical solution, and the maximum percentage of error was around 3%.
1. 서 론
Friction Stir Welding(FSW)은 1991년 The Welding Institute(TWI)에서 개발된 후1) 용접 결함이 적으며 기존 방법으로 용접이 힘들던 알루미늄 박판과 같은 소재에 적용이 가능하며 고상용접이기 때문에 용접부의 품질도 우수한 새로운 용접기술로서 많은 연구가 진행되고 있다2).
FSW에서는 툴 형상 및 회전속도 등의 여러 조건에 따라 용접성이 달라지기 때문에 보다 최적의 실험조건을 찾기 위해서는 해석적인 연구가 반드시 선행되어야 한다. 그중 Computational Fluid Dynamics(CFD)해석은 실험으로 파악하기 힘든 유동장의 묘사가 가능하고, 실제 FSW의 물리적인 현상들을 잘 반영하는 해석방법으로 많은 연구자들이 택하고 있다. 하지만 공정 중 발생하는 마찰에 의한 열원과 소성변형에 의한 열원을 모두 표현하기가 힘들기 때문에 기존의 연구자들은 다음과 같은 방법으로 열원을 모델링하였다. Kim 외3)는 상용코드인 STAR-CCM+를 이용하여 CFD해석을 수행하였다. 해석에서 얻은 온도이력이 측정치와 잘 일치하는 결과를 얻었지만, 툴과 모재간의 마찰에 의한 열원을 고려하지 않았다. 열원으로 소성변형에 의해 발생하는 열량만을 고려하였는데, 소성변형이 열량으로 전달되는 비를 1로 계산하였다. Chen 외4)는 상용코드인 ANSYS Fluent를 이용해서 해석을 진행하였는데 툴의 이동속도가 일정할 때, 회전속도에 따른 총 발열량의 관계를 수식화 하였다. 그의 논문에서도 표면 마찰에 따른 열원을 고려하지 않고 소성변형에 의한 열량만을 고려하였는데, 비를 0.8로 계산하였다. Ji 외5)는 ANSYS Fluent를 이용해 툴 형상이 유동장에 미치는 영향을 조사하였는데, 열원을 고려하기 위해서 툴의 표면에 기존의 관념으로 알려진 융점의 80%온도를 경계조건으로 주었다. 이처럼 기존 CFD접근법에서는 많은 경우 표면마찰에 의한 열원을 고려하지 않고 소성변형에 의한 열원만을 이용해 문제를 해결하였고, 마찰 열원을 고려한 논문에서도 툴의 회전과 이동을 묘사하는데 어려움이 있어 경계조건을 적용하는 등의 여러 방법 이용하였다.
따라서 본 연구에서는 툴의 회전 및 이동을 동시에 고려하고 그에 따른 마찰열원을 적용하기 위해 실시간으로 표면을 추적하는 알고리즘을 제시하였다. 해석결과를 이론적으로 구한 마찰열원의 크기와 비교하면서 검증하였다.
2. 표면추적 및 표면적 계산
2.1 표면추적
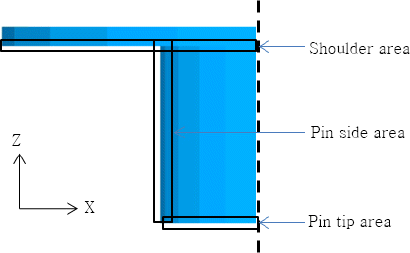
툴이 회전하면서 동시에 이동하기 때문에, 본 연구에서는 툴의 표면을 추적하기 위해서 Table 1과 같이 접근하였다. Table 1에서 rp 및 rs 는 각각 숄더와 핀의 반지름이며, Δcell은 셀의 크기이며 x는 툴 중심에서부터 임의의 셀 중심까지의 거리이다. 각 영역의 표면 셀 추적원리는 다음과 같다. 실린더 형상의 툴은 대칭이기 때문에 항상 툴의 중심에서부터 임의의 표면까지 거리를 알 수 있다. 예를 들어 툴의 중심에서 핀 측면까지의 거리는 항상 핀의 반경과 같으며, 숄더의 측면까지는 항상 숄더의 반경과 같다. 따라서 매 순간 툴의 중심의 좌표에서 임의의 셀까지의 거리를 모두 계산하여 그 거리가 Table 1에서 제시된 영역내로 계산이 되면, 해당 셀들은 표면 셀로 인식하게 되는 것이다. 또한 각 반경인 rp 및 rs 에서 셀 크기의 절반만큼 더하거나 빼주는 이유는 셀이 3차원이고 툴의 표면은 2차원이므로 툴의 표면이 3차원의 셀 내에서 움직이는 경우까지 포함하기 위함이다. 계산을 위해 분할된 숄더, 핀 측면 및 핀 밑면 영역은 Fig. 1과 같다.
2.2 표면적 계산
표면추적을 통해 얻어진 표면 셀을 이용하여 마찰 열원을 부여하기 위해서는 모든 표면 셀에서 툴과 모재가 접촉하는 표면적을 계산하여야 한다. 하지만 툴의 회전과 이동을 모두 고려하면서 정확한 표면적을 계산하는데 어려움이 있어 본 연구에서는 평균 표면적의 개념으로 접근하였다. 이를 위해 먼저 툴과 모재가 만나는 면적을 계산하고, 그 면적을 매 순간마다 앞서 설명한 표면추적방법으로부터 얻어진 표면 셀의 개수로 나누었다. 그러면 한 표면 셀 당 평균적으로 접촉하는 면적을 계산할 수 있는데, 모든 표면 셀에서 이 평균면적이 작용한다고 가정하였다. 이러한 방법으로 얻은 데이터를 3.4절에서 설명한 열원 모델링에 적용하면서 마찰열원을 해석적으로 구하였다.
3. 모델링
3.1 가정
표면 마찰에 의한 열원을 이론식으로 구한 값과 비교하기 위해서, 해석은 처음부터 툴이 모재에 삽입되어 있는 상태에서 진행되었다. 해석이 진행되는 동안 툴은 강체로 가정하여 변형이 없으며, 툴의 회전속도와 이동속도는 일정한 값을 유지하였다. 모재는 점성이 큰 유체로 가정하였고, 하나의 모재의 중심부에 용접이 진행되는 조건을 사용하였다.
3.2 툴 형상 모델링
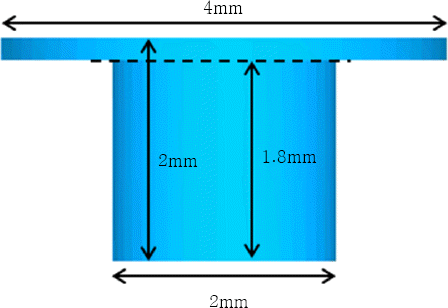
Fig. 2와 같이 비교적 단순한 형태의 툴이 고려되었는데, 이는 이론적으로 마찰에 의한 열량을 구할 수 있기 때문이다. 또한 제안하는 표면추적 알고리즘을 가장 단순화된 형태의 툴에 적용해 검증을 마친 후, 보다 복잡한 툴 형상에 적용할 수 있도록 모델을 개발하고자 함에 있다.
3.3 점성계수 모델링
FSW에서 점성계수는 온도와 스트레인 변화율의 함수로 표현되며, 점성계수를 계산하기 위해서 먼저 Sheppard 외6)가 제안한 유동응력(flow stress)을 다음으로 구한다.
여기서 A, α, n은 재료상수이며 실험을 통해서 측정된다. 본 연구에서는 모재로 AA5052-O를 사용하였고 해당 모재의 재료상수는 Table 2에 표기하였다. Z는 Zener-Hollomon parameter 이며 다음으로 표현된다.
여기서 Q는 활성화 에너지(activation energy), R은 기체상수, T는 온도를 나타내며, ∈·는 실질적인 스트레인 변화율(effective strain rate)로서 다음으로 표현된다.
여기서 ∈ij는 스트레인 변화율 텐서로 다음으로 정의된다.
점성계수는 유동응력과 실질적인 스트레인 변화율의 함수로 표현되는 Perzyna의 점소성 모델(visco-plasticity model)7)에 따라 다음으로 표현된다.
위의 표현식처럼, 점성계수는 온도와 스트레인 변화율에 의해 지배받게 된다. 따라서 적절한 열원 모델링은 온도분포 뿐만 아니라, 점성계수 및 유동장에도 영향을 미치는 것을 알 수 있다.
3.4 열원 모델링
FSW공정에서는 마찰에 의한 열원과 소성변형에 의한 열원이 발생하게 된다. 그중 마찰에 의한 열원 Sfric은 다음과 같이 표현된다.
여기서 m은 마찰인자(friction factor)는 항복에서 최대 전단응력 (maximum shear stress at yielding)으로 이 값은 Von-Mises 이론에 따르면
소성변형에 의한 열원 Spd 는 다음과 같이 표현된다9,10).
여기서 fm 은 열로 전달되는 비로 0.04가 적용되었다11).
앞서 설명한 표면추적알고리즘과 더불어 열원 및 점성 등의 관계식들을 적용한 해석을 수행하기 위해 해석프로그램인 Flow-3D의 유저 서브루틴(user subroutine)을 이용하여 해석을 수행하였다.
3.5 경계조건 모델링
FSW의 특성상, 용접이 진행될 때 툴이 모재를 강하게 누르기 때문에 모재의 바닥에 받침용 판(backing plate)을 두게 된다. 따라서 모재의 바닥면에서는 모재와 받침용 판 사이에 전도에 의한 열전달이 일어나지만, 전도계수를 정하는 어려움으로 인해 동등한 대류가 일어난다고 가정하고 경계조건을 적용하였다13). 그 외의 영역에서는 모재와 대기가 접촉하고 있기 때문에 대류 및 복사조건을 적용하였다.
4. 결 과
4.1 이론적인 해
모델을 검증하기 위해 본 연구에서는 Schmidt 외14)에서 제시한 이론적인 계산법(analytical model)으로 마찰열원의 크기를 구하였다. 해당 논문에서는 본 연구에서 사용되었던 것과 같은 실린더 형상 툴의 기하학적 관계를 기초로 구하였는데, 각 표면(숄더 및 핀)에 작용하는 미소 마찰력을 전 영역에 대해 적분하면서 구하였다. 이때 마찰력을 표현하는 방법은 해당 논문의 모델링 파트에서 사용했던 표현과 유사한 방법을 택하였다. 이러한 방법을 통해 해당 툴을 각각 숄더, 핀 옆면, 핀 밑면으로 나눈 후 마찰열원을 구한 결과는 Table 3과 같다. 숄더에서 가장 큰 열이 발생을 하고, 핀 옆면, 핀 밑면 순으로 열원의 크기가 컸다. 그 이유는 숄더에서 가장 많은 접촉면적을 가지고 있기 때문이다. 또한 숄더의 반경이 핀보다 더 크기 때문에, 반경에 따라 비례하는 속도의 영향이 고려되었기 때문이다.
4.2 이론적인 해와 비교
해석결과는 Fig. 3과 같다. 마찰열원은 툴의 회전속도에 비례하기 때문에 툴의 중심에서 멀어질수록 그 열원의 크기가 커야하며 해석결과는 이러한 경향을 잘 나타내고 있다. 또한 핀의 밑면 중 툴의 중심부는 회전속도가 0에 가깝기 때문에 발생하는 열량이 아주 작음을 확인할 수 있다. 해석시간을 선정하기 위해 처음 위치에서 툴의 크기만큼 이동하는 시간을 고려하였다. 즉 숄더의 지름을 근거로 하여 4mm를 이동하는 시간만큼 해석을 진행하였고, 그때의 해석시간은 0.24s이었다.
툴이 회전하면서 동시에 이동하기 때문에, 매 사이클마다 표면 셀의 개수는 달라진다. 따라서 충분히 많은 수의 데이터를 얻은 후 그 값들을 분석하기 위해 4mm동안 이동시켰다. 총 해석시간인 0.24s를 1/5000s로 분할하면 총 1200개의 데이터를 얻는데, 이 데이터를 평균하였고 그 결과를 수치해로 정하였다. 그 결과는 Table 4와 같은데, 해석결과 역시 숄더, 핀 옆면, 핀 밑면 순으로 열원의 크기가 나타남을 확인할 수 있으며 모든 형상에서 같은 경향을 나타났다. 해석결과와 이론값과의 비교는 Table 5와 같다. 핀 밑면에서는 약 10%가량의 오차가 나타났는데, 이는 핀 밑면에서 발생하는 열량의 절대적인 크기가 작기 때문이다. 반면에 숄더와 핀 옆면에서는 0.7~2.7%가량의 오차가 나타났으며, 총 열량과의 비교에서는 1%내외의 오차가 나타났다.
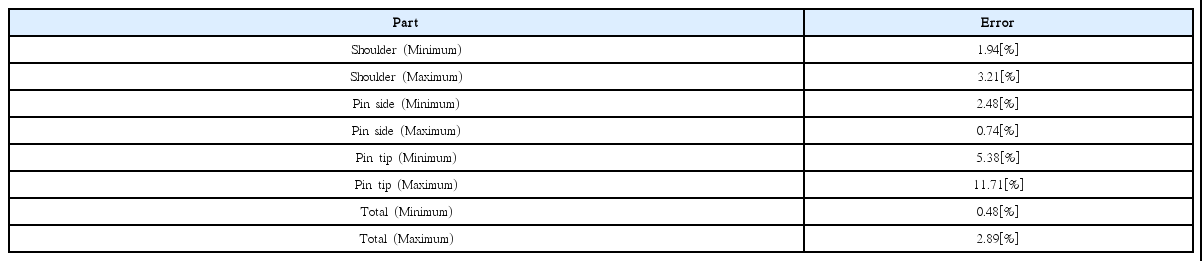
해석이 진행되는 동안에 표면 셀의 개수는 매번 변하게 된다. 즉 표면에서 발생하는 열량 역시 매번 변함을 의미한다. 본 연구에서는 총 1200개 데이터의 평균값을 수치해로 정하였는데, 그 평균값의 타당성을 알아보기 위해 총 1200개 데이터의 최소 및 최대값과 이론적인 값과의 결과를 추가로 비교하였다. Table 6에서처럼 평균값보다는 최소값을 이용하였을 때 더 이론값과 근접하는 것을 확인할 수 있지만 그 차이는 1%내외이며, 가장 큰 오차를 수반했던 최대값을 이용한 경우에도 오차는 3%이하로 나타났다. 따라서 어떤 변수를 택하건 최대 오차는 3%이하로 발생하기 때문에 충분히 이론적인 결과와 일치한다고 볼 수 있으며, 본 연구에서 사용했던 평균값을 이용한 접근이 타당함을 확인할 수 있다.
5. 결 론
기존 마찰교반용접의 전산유체역학을 이용한 해석과는 달리, 툴의 회전과 이동을 표현하면서 동시에 마찰열원을 부여하기 위해 새로운 알고리즘을 제안하였다. 매 사이클마다 표면 셀을 추적하고 평균표면적을 적용하면서 마찰열원을 임의의 시간과 위치에서도 부여할 수 있었다. 해석결과는 이론적인 값과 3%내외의 오차를 보였으며 평균값을 사용했을 땐, 1%가량의 오차를 보였다.
따라서 툴의 형상에 맞춰 표면 셀을 찾고 그 면적을 구하기 위해 평균면적의 개념을 적용하는 것은 합당한 가정이었음을 확인할 수 있었다. 본 알고리즘을 이용 및 개발하여 향후 임의의 툴 형상에 대해 마찰열원을 보다 정확히 묘사할 수 있는데 도움이 될 것으로 기대한다.