| J Weld Join > Volume 37(1); 2019 > Article |
Abstract
The purpose of this study is to quickly and accurately predict the deformed shape of the curved plate located before and after the surface of the hull manufactured by multi line heating (or flame bending). Three dimensional thermo-elasto-plastic analysis takes long time and requires userŌĆÖs guidance to simulate the deformation. To overcome these drawbacks, this study employed the SDB(Strain as Direct Boundary) method based on thermal strain rather than the three dimensional finite element analysis using solid element. The thermal strain, including material phase transformation and volumetric expansion occurred during Martensite phase transformation, is specially considered by SDB. This study calculates the temperature dependent phase portion using material chemical composition and reflects the martensite portion dependent volumetric expansion. The Heat Affected Zone(HAZ) is obtained by thermal analysis and virtual temperature substituting the heat input is assumed by the size and shape of HAZ. In order to reflect the initial deformation due to the former heating lines to the post-deformation analysis, this study predicts the deformation by multi-line heating using the plastic material properties. Thereafter, comparing the deformation of the plate with the 3D solid elasto-plastic analysis and the SDB method, this study shows the accuracy and efficiency of the SDB method.
ICTļź╝ ĒÖ£ņÜ®ĒĢ£ ņ¦ĆļŖźĒśĢ ņĀ£ņĪ░ ĻĖ░ņłĀņØ┤ ĒÖĢņé░ļÉśļ®┤ņä£ ņĪ░ņäĀ ņé░ņŚģ ļśÉĒĢ£ ņ¦ĆļŖźĒśĢ ņāØņé░ ĻĖ░ņłĀņØ┤ ĒÖĢļīĆĒĢśĻ│Ā ņ׳ļŗż. ņØ┤ļ¤¼ĒĢ£ ĻĖ░ņłĀņØĆ ļŗżņ¢æĒĢ£ ņäĀļ░Ģ ņāØņé░ Ļ│ĄņĀĢņŚÉ ņĀüņÜ®ĒĢśĻ│Ā ņ׳ņ£╝ļéś, ņŚ¼ņĀäĒ׳ ņäĀņ▓┤ ņÖĖĒīÉņØś Ļ│Īļ®┤ Ļ░ĆĻ│ĄņØĆ ņ×ÉļÅÖĒÖö ņ×Éņ▓┤Ļ░Ć ņ¢┤ļĀżņÜ┤ Ļ│ĄņĀĢņŚÉ ņåŹĒĢ£ļŗż. Ļ░ĆĻ│Ą ņ×æņŚģņ×ÉņØś Ļ▓ĮĒŚś ņ¦ĆņŗØņŚÉ ņØśņĪ┤ĒĢśļŖö Ļ│Īļ®┤ Ļ░ĆĻ│ĄņØś ļŗ©ņĀÉņØä ĻĘ╣ļ│ĄĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ņŚ¼ļ¤¼ Ļ░Ćņ¦ĆņØś ļ│ĆĒśĢ ņśłņĖĪļ▓ĢĻ│╝ ņ×ÉļÅÖĒÖö ļ░®ļ▓ĢņØ┤ ņŗ£ļÅäļÉśņŚłļŗż1-5). ņŚ┤Ļ░äĻ░ĆĻ│Ą ņ×ÉļÅÖĒÖöļź╝ ņ£äĒĢ┤ņä£ Ļ░Ćņן ļ©╝ņĀĆ ņäĀĒ¢ēļÉśņ¢┤ņĢ╝ ĒĢĀ Ļ▓āņØĆ ļ¬®Ēæ£ĒĢśļŖö Ļ│Īļ®┤ ĒśĢņāüņŚÉ ļÅäļŗ¼ĒĢśĻĖ░ ņ£äĒĢ£ Ļ░ĆņŚ┤ņäĀĻ│╝ ļ│ĆĒśĢņØä ņśłņĖĪņØ┤ļŗż. ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö ņĀ£ņŗ£ļÉ£ Ļ░ĆņŚ┤ņäĀņØś Ļ▓Ćņ”Ø Ļ│╝ņĀĢ ņżæņŚÉņä£ ļŗżņżæ Ļ░ĆņŚ┤ņäĀņØä ņĀüņÜ®ĒĢśņśĆņØä ļĢī ļéśĒāĆļéśļŖö Ļ│Īļ®┤ņØś ņĄ£ņóģ ĒśĢņāüņØä ĒÜ©Ļ│╝ņĀüņ£╝ļĪ£ ņśłņĖĪĒĢśĻĖ░ ņ£äĒĢ£ ļ░®ņĢłņØä ņĀ£ņŗ£ĒĢśĻ│Āņ×É ĒĢ£ļŗż.
Ļ░ĆņŚ┤ņŚÉ ņØśĒĢ£ ļ│ĆĒśĢ ĒśĢņāüņØä ņśłņĖĪĒĢ©ņŚÉ ņ׳ņ¢┤ņä£ Ļ░Ćņן ņØ┤ļĪĀņĀüņØĖ ļ░®ļ▓ĢņØĆ ņŚ┤ņĀäļŗ¼ ļ░Å ņåīņä▒ļ│ĆĒśĢ ĒśäņāüņØä Ļ│ĀļĀżĒĢ£ ņ£ĀĒĢ£ņÜöņåīĒĢ┤ņäØņØ┤ļŗż. ĻĘĖļ¤¼ļéś ņØ┤ ļ░®ļ▓ĢņØĆ ņ╗┤Ēō©Ēä░ņØś ņŚ░ņé░ ņåŹļÅäņØś ņ”ØĻ░ĆņŚÉļÅä ļČłĻĄ¼ĒĢśĻ│Ā ņłś ņŗ£Ļ░ä ņØ┤ņāüņØś Ļ│äņé░ ņŗ£Ļ░äņØä ĒĢäņÜöļĪ£ ĒĢĀ ļ┐Éļ¦ī ņĢäļŗłļØ╝ Ļ░ĆņŚ┤ņäĀ ņ£äņ╣śļź╝ Ļ│ĀļĀżĒĢśņŚ¼ ņŗżņŗ£Ļ░äņ£╝ļĪ£ Ļ░ĆņŚ┤ņäĀ Ļ│äņé░Ļ│╝ ļ│ĆĒśĢ ņśłņĖĪņØä ņłśĒ¢ēĒĢ┤ņĢ╝ Ļ│╝ņĀĢņØä ņ×ÉļÅÖņ£╝ļĪ£ ņłśĒ¢ēĒĢśļŖö Ļ▓āņØ┤ ņ¢┤ļĀĄļŗż. ĻĘĖļ¤¼ļ»ĆļĪ£ ņØ┤ļ¤¼ĒĢ£ ļŗ©ņĀÉņØä ļ│┤ņÖäĒĢśņŚ¼ ņŗĀņåŹĒĢśĻ▓ī ļ│ĆĒśĢņØä ņśłņĖĪĒĢĀ ņłś ņ׳ļŖö Ļ░äņØ┤ ĒĢ┤ņäØļ▓ĢņØ┤ ĒĢäņÜöĒĢśļŗż.
ļŗżņżæņØś ņØ┤ļÅÖ ņŚ┤ņøÉņŚÉ ņØśĒĢ£ ļ│ĆĒśĢņØä ņŗĀņåŹĒĢśĻ▓ī ņśłņĖĪĒĢśļŖö ļ░®ļ▓Ģņ£╝ļĪ£ Ļ░Ćņן ļīĆĒæ£ņĀüņØĖ Ļ▓āņØ┤ Ļ│Āņ£Āļ│ĆĒśĢļźĀņØä ņØ┤ņÜ®ĒĢ£ ļō▒Ļ░ĆĒĢśņżæļ▓Ģ1)ņØ┤ļŗż. ņØ┤ļŖö ņ×äĻ│äņś©ļÅä ņØ┤ņāüņØä Ļ▓¬ņØĆ ņśüņŚŁņØä ņśüĻĄ¼ņĀüņØĖ ļ│ĆĒśĢņØ┤ ļé©ļŖö ņŚ┤ņśüĒ¢źļČĆļĪ£ Ļ░ĆņĀĢĒĢśĻ│Ā, Ļ│Āņ£Ā ļ│ĆĒśĢļźĀņØä ļō▒Ļ░ĆĒĢśņżæņ£╝ļĪ£ ņ╣śĒÖśĒĢśņŚ¼ Ēāäņä▒ ĒĢ┤ņäØļ¦īņ£╝ļĪ£ ļ│ĆĒśĢņØä ņśłņĖĪĒĢśļŖö ļ░®ļ▓ĢņØ┤ļŗż. ĻĘĖļ¤¼ļéś ņØ┤ ļ░®ļ▓ĢņØĆ Ļ│Āņ£Āļ│ĆĒśĢļźĀ Ļ│äņé░ņŚÉ ņ׳ņ¢┤ņä£ ņ×¼ļŻīņØś Ļ░Ģņä▒ņØ┤ļéś ņØ┤ļ░®ņä▒ ņĀĢņØśĻ░Ć ļ▓łĻ▒░ļĪŁļŗż. ļśÉĒĢ£ Ļ░ĆņŚ┤ņäĀņØä ļō▒Ļ░Ć ĒĢśņżæĻ│╝ ļ¬©ļ®śĒŖĖļĪ£ ņ╣śĒÖśĒĢśņŚ¼ Ļ▓ĮĻ│äņĪ░Ļ▒┤ņ£╝ļĪ£ ņĀüņÜ®ļÉśĻĖ░ ļĢīļ¼ĖņŚÉ ļ│ĆĒśĢ ĒĢ┤ņäØ ļ¬©ļŹĖņØä ĻĄ¼ņä▒ĒĢ©ņŚÉ ņ׳ņ¢┤ņä£ ņ×ÉļÅÖĒÖöļÉ£ ĒĢśņżæ ļ░®Ē¢źĻ│╝ Ēü¼ĻĖ░ņØś ņĀĢņØśĻ░Ć ņ¢┤ļĀĄļŗż. ļö░ļØ╝ņä£ ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö ņ×öļźś ļ│ĆĒśĢļźĀņØä ņēś ņÜöņåīņØś ņŚ┤ĒīĮņ░Į Ļ│äņłśļĪ£ ņĀüņÜ®ĒĢśĻ│Ā, ņśüĒśĢĒ¢źļČĆņØś ĒśĢņāüņŚÉ ļö░ļźĖ ļō▒Ļ░Ćņś©ļÅäļź╝ Ļ│äņé░ĒĢśņŚ¼ ņØ┤ļź╝ Ļ░ĆņŚ┤ņäĀņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö ņĀłņĀÉņŚÉ Ļ▓ĮĻ│äņĪ░Ļ▒┤ņ£╝ļĪ£ ņĀüņÜ®ĒĢśļŖö ļ│ĆĒśĢļźĀ Ļ▓ĮĻ│äļ▓Ģ(SDB)ņØä ņé¼ņÜ®ĒĢśņśĆļŗż3).
Ļ│Āņś©ņØś ņŚ┤ņØä Ļ▓¬ļŖö ņŚ┤Ļ░äĻ░ĆĻ│ĄņØś Ļ▓ĮņÜ░ ņāüļ│ĆĒā£2)Ļ░Ć ļČłĻ░ĆĒö╝ĒĢśĻ▓ī ņØ╝ņ¢┤ļéśĻ▓ī ļÉśļŖöļŹ░, ĒŖ╣Ē׳ Ļ░ĆņŚ┤Ļ│╝ņĀĢņŚÉņä£ ņśżņŖżĒģīļéśņØ┤ĒŖĖļĪ£ ļ│ĆĒā£ĒĢ£ ņāüņØ┤ ļ╣ĀļźĖ ļāēĻ░ü Ļ│╝ņĀĢņ£╝ļĪ£ ņØĖĒĢ┤ ļ¦łļź┤ĒģÉņé¼ņØ┤ĒŖĖļĪ£ ļ│ĆĒā£ĒĢśĻ▓ī ļÉ£ļŗż. ņØ┤ Ļ│╝ņĀĢņŚÉņä£ ņØ╝ņ¢┤ļéśļŖö ļČĆĒö╝ļ│ĆĒÖöļŖö ņ×öļźś ļ│ĆĒśĢļźĀņŚÉ ņśüĒ¢źņØä ļ»Ėņ╣śĻ▓ī ļÉ£ļŗż. ļĢīļ¼ĖņŚÉ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņ×¼ļŻīņØś ĒÖöĒĢÖ ņä▒ļČäļźĀņØä ņØ┤ņÜ®ĒĢ┤ Ļ░ü ņś©ļÅäņŚÉ ļö░ļźĖ ņāüņØś ļČäņ£©ņØä Ļ│äņé░ĒĢśĻ│Ā, ļ¦łļź┤ĒģÉņé¼ņØ┤ĒŖĖ ļČäņ£©ņŚÉ ļö░ļźĖ ļČĆĒö╝ ĒīĮņ░ĮņØä ņ×¼ļŻīņØś ļ│ĆĒśĢņ£©ņŚÉ ļ░śņśüĒĢśņŚ¼ ļ│ĆĒśĢ ņśłņĖĪņØś ņĀĢĒÖĢļÅäļź╝ ļåÆņØ┤Ļ│Āņ×É ĒĢśņśĆļŗż. Ļ░ĆņŚ┤ņŚÉ ļö░ļźĖ ĒīÉņØś ņŚ┤ņśüĒ¢źļČĆļŖö ņŚ┤ņøÉņØś ņØ┤ļÅÖņŚÉ ļö░ļźĖ ņŚ┤ņĀäļŗ¼ ĒĢ┤ņäØņØä ĒåĄĒĢ┤ ņ¢╗ņŚłņ£╝ļ®░, ņ×äĻ│äņś©ļÅäļŖö ņ×¼ļŻīņØś ņä▒ļČäĒĢ©ļ¤ēņŚÉ ļö░ļØ╝ Ļ│äņé░ļÉ£ Ļ░ÆņØä ņé¼ņÜ®ĒĢśņśĆļŗż4). ļśÉĒĢ£ ņŚ┤Ļ░äĻ░ĆĻ│ĄņØś Ļ▓ĮņÜ░ Ļ░ĆņŚ┤ņäĀņØ┤ ņŚ¼ļ¤¼ Ļ░£ņØĖ Ļ▓ĮņÜ░Ļ░Ć ļ│┤ĒÄĖņĀüņØ┤ļŗż. ļö░ļØ╝ņä£ ņØ┤ņĀä Ļ░ĆņŚ┤ņäĀņØś ņśüĒ¢źņØä ļ░śņśüĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ņ×¼ļŻīļź╝ ņåīņä▒ņ£╝ļĪ£ Ļ░ĆņĀĢĒĢśļŖö ņŚ┤ļ│ĆĒśĢļźĀ ĻĖ░ļ░ś Ēāäņåīņä▒ ĒĢ┤ņäØ ļ░®ļ▓ĢņØä ņé¼ņÜ®ĒĢśņśĆļŗż5,11).
ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö ņ¦ĆĻĖłĻ╣īņ¦Ć ņĀ£ņŗ£ļÉ£ ņØ┤ļÅÖ ņŚ┤ņøÉņŚÉ ņØśĒĢ£ ĒīÉņØś ņ×öļźś ņŚ┤ļ│ĆĒśĢņØä ņśłņĖĪĒĢśļŖö ļ░®ļ▓Ģ ņżæ Ļ░Ćņן ņĀüĒĢ®ĒĢśļŗżĻ│Ā ĒīÉļŗ©ļÉśļŖö ņŚ┤ļ│ĆĒśĢļźĀ ĻĖ░ļ░śņØś Ēāäņåīņä▒ ļ│ĆĒśĢļźĀ Ļ▓ĮĻ│äļ▓ĢņØä ņóģĒĢ®ņĀüņ£╝ļĪ£ ņĀĢļ”¼ĒĢśņŚ¼ ņĀüņÜ®ĒĢśņśĆļŗż. ĻĘĖļ”¼Ļ│Ā ņ£ä ļ░®ļ▓ĢņØś ĒÜ©ņ£©ņä▒Ļ│╝ ņĀĢĒÖĢņä▒ņØä Ļ▓Ćņ”ØĒĢśĻĖ░ ņ£äĒĢśņŚ¼ 3ņ░©ņøÉ ņåöļ”¼ļō£ ņÜöņåīļź╝ ņé¼ņÜ®ĒĢ£ ņŚ┤Ēāäņåīņä▒ ĒĢ┤ņäØņ£╝ļĪ£ ĻĄ¼ĒĢ£ ļ│ĆĒśĢ ĒśĢņāüņØä ļ╣äĻĄÉĒĢśņśĆļŗż.
ļ│ĆĒśĢ ĒĢ┤ņäØļ▓ĢņŚÉļŖö Ļ░Ćņן ņØ╝ļ░śņĀüņ£╝ļĪ£ ņ£ĀĒĢ£ņÜöņåī ĒĢ┤ņäØņØś ņåöļ”¼ļō£ ņÜöņåīļź╝ ņé¼ņÜ®ĒĢ£ ņŚ┤Ēāäņåīņä▒ ĒĢ┤ņäØ ļ░®ļ▓ĢņØ┤ ņ׳ļŗż. ņ£ä ļ░®ļ▓ĢņØĆ ņŚ┤ņĀäļŗ¼ ĒĢ┤ņäØņØä ĒåĄĒĢ┤ ņŚ┤ņøÉņØś ņØ┤ļÅÖņŚÉ ļö░ļźĖ ĒīÉņØś ņś©ļÅä ņØ┤ļĀźņØä Ļ│äņé░ĒĢ£ Ēøä, ņØ┤ņŚÉ ļö░ļźĖ ĒīÉņØś ļ│ĆĒśĢņØä Ēāäņåīņä▒ ĒĢ┤ņäØņØä ĒåĄĒĢ┤ ļÅäņČ£ĒĢśĻ▓ī ļÉ£ļŗż. ņØ┤ ļ░®ļ▓ĢņØĆ ņŚ┤ņøÉņØś ĒśĢņāüĻ│╝ Ēü¼ĻĖ░ļź╝ ļ¬©ļæÉ ņĀĢņØśĒĢśĻ│Ā ņś©ļÅäņŚÉ ļö░ļźĖ ņ×¼ļŻīņØś ļ¼╝ņä▒ņ╣śļź╝ ļ¬©ļæÉ Ļ│ĀļĀżĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ ņĀĢĒÖĢĒĢ£ ņśłņĖĪņØ┤ Ļ░ĆļŖźĒĢśĻ│Ā, ļāēĻ░ü Ēøä ņ×öļźś ņØæļĀź ļśÉĒĢ£ ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż. ĒĢśņ¦Ćļ¦ī ņ╗┤Ēō©Ēä░ ĒĢśļō£ņø©ņ¢┤ņØś ļ░£ņĀäņŚÉļÅä ļČłĻĄ¼ĒĢśĻ│Ā ņŚ┤Ēāäņåīņä▒ ĒĢ┤ņäØņØĆ ņŚ¼ņĀäĒ׳ ņłś ņŗ£Ļ░äņØś ĒĢ┤ņäØ ņŗ£Ļ░äņØä ņÜöĻĄ¼ĒĢ£ļŗż. ĻĘĖļ¤¼ļ»ĆļĪ£ ņŗĀņåŹĒĢ£ ņśłņĖĪņØ┤ Ļ░ĆļŖźĒĢ£ ņēś ņÜöņåīļź╝ ņØ┤ņÜ®ĒĢ£ ļ│ĆĒśĢļźĀ ĻĖ░ļ░ś ļō▒Ļ░Ć Ļ▓ĮĻ│äņĪ░Ļ▒┤ ļ░®ļ▓ĢņØä ņØ┤ņÜ®ĒĢśļŖö Ļ▓āņØ┤ ĒĢ┤ņäØņŗ£Ļ░äņØä ļŗ©ņČĢĒĢĀ ņłś ņ׳ļŗż. ļīĆĒæ£ņĀüņØĖ ņé¼ņÜ® ļ│ĆĒśĢļźĀņØĆ Ļ│Āņ£Ā ļ│ĆĒśĢļźĀĻ│╝ ņŚ┤ļ│ĆĒśĢļźĀņØ┤ ņ׳ņ£╝ļ®░, ļō▒Ļ░Ć Ļ▓ĮĻ│äņĪ░Ļ▒┤ ļ░®ļ▓ĢņØĆ ļō▒Ļ░ĆĒĢśņżæļ▓ĢĻ│╝ ļ│ĆĒśĢļźĀ Ļ▓ĮĻ│äļ▓ĢņØ┤ ņ׳ļŗż. ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņŚ┤ļ│ĆĒśĢļźĀņŚÉ ĻĖ░ļ░śĒĢ£ ļ│ĆĒśĢļźĀ Ļ▓ĮĻ│äļ▓ĢņØä ņØ┤ņÜ®ĒĢśņŚ¼ ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśņśĆļŗż.
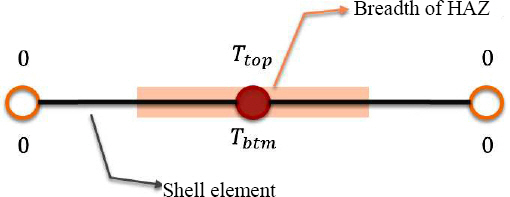
ņŚ┤ņøÉņŚÉ ņØśĒĢ£ ĒīÉņØś ļ│ĆĒśĢņØĆ ņŚ┤ņśüĒ¢źļČĆ(HAZ)ļź╝ ņżæņŗ¼ņ£╝ļĪ£ ņØ╝ņ¢┤ļé£ļŗż. ņ×öļźś ļ│ĆĒśĢļźĀņØ┤ ņāØņä▒ļÉśļŖö Ļ│╝ņĀĢņØä 2ļŗ©Ļ│äļĪ£ ļéśļłī ņłś ņ׳ļŖöļŹ░, Ļ│Āņś©ņØś ņŚ┤ņØä Ļ▓¬ļŖö Ļ░ĆņŚ┤ļŗ©Ļ│äņÖĆ Ļ│Āņś©ņŚÉņä£ ņāüņś©ņ£╝ļĪ£ ņŗØņ¢┤Ļ░ĆļŖö ļāēĻ░üļŗ©Ļ│äļĪ£ ļéśļłī ņłś ņ׳ļŗż.
ļ©╝ņĀĆ Ļ░ĆņŚ┤ļŗ©Ļ│äņŚÉņä£ļŖö ņ×¼ļŻī ĒŖ╣ņä▒ņāü ĒĢŁļ│ĄņØæļĀźĻ│╝ Ēāäņä▒Ļ│äņłśĻ░Ć 0ņŚÉ Ļ░ĆĻ╣īņøīņ¦ĆĻĖ░ ļĢīļ¼ĖņŚÉ ņåīņä▒ ņØæļĀźĻ│╝ ļ│ĆĒśĢļźĀņØ┤ ļ░£ņāØĒĢśņ¦Ć ņĢŖļŖöļŗżĻ│Ā Ļ░ĆņĀĢĒĢśņśĆļŗż. ĻĘĖļ¤¼ļ»ĆļĪ£ ĒīÉņØś ļ│ĆĒśĢņØĆ ļāēĻ░üļŗ©Ļ│äļź╝ ņżæņŗ¼ņ£╝ļĪ£ ņØ╝ņ¢┤ļéśĻ▓ī ļÉ£ļŗż. ņØ┤ļĢī ļ░£ņāØĒĢśļŖö ņŚ┤ļ│ĆĒśĢļźĀņØä ņŚ┤ņśüĒ¢źļČĆņØś ņ┤łĻĖ░ ļ│ĆĒśĢļźĀļĪ£ Ļ░ĆņĀĢĒĢśĻ│Ā, ņŻ╝ļ│ĆļČĆļź╝ ņŚ┤ ņśüĒ¢źļČĆļź╝ ĻĄ¼ņåŹĒĢśļŖö ņÜöņåīļĪ£ Ļ░ĆņĀĢĒĢśņŚ¼ ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢśņśĆļŗż.
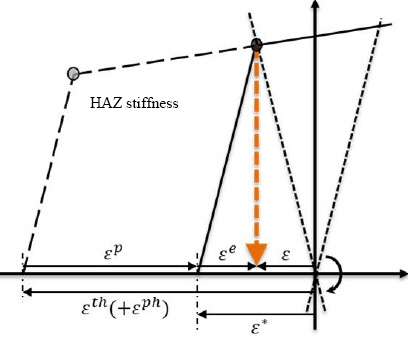
ņ£ä ņŗØ(1)ņØĆ Ļ│Āņ£Āļ│ĆĒśĢļźĀ(ŽĄ)ņØä ņ┤Øļ│ĆĒśĢļźĀ(ŽĄ)Ļ│╝ Ēāäņä▒ļ│Ć ĒśĢļźĀ(ŽĄe), ņåīņä▒ļ│ĆĒśĢļźĀ(ŽĄp)Ļ│╝ ņŚ┤ļ│ĆĒśĢļźĀ(ŽĄth)Ļ│╝ ņāüļ│ĆĒā£ļ│Ć ĒśĢļźĀ(ŽĄph)ļĪ£ Ēæ£ĒśäĒĢ£ ņŗØņØ┤ļŗż5). ņØ┤ Ļ┤ĆĻ│äļź╝ Fig. 1ņŚÉ ļéśĒāĆ ļāłļŗż.
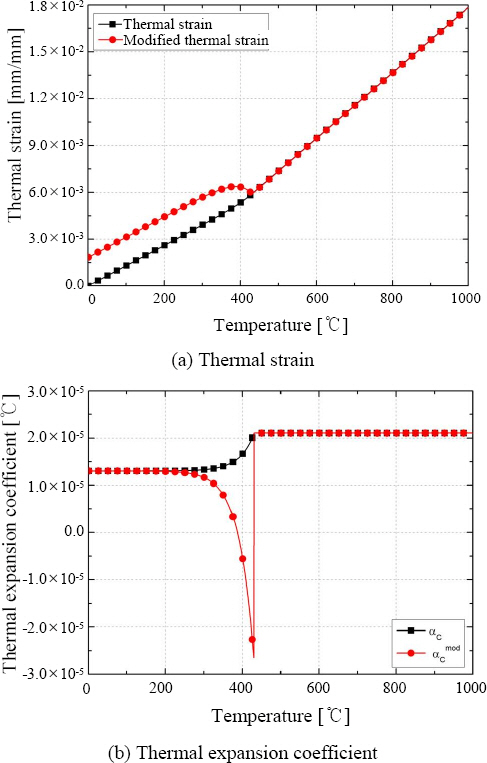
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņāüļ│ĆĒā£ļź╝ ĒżĒĢ©ĒĢśļŖö ņŚ┤ļ│ĆĒśĢļźĀņØä ņŚ┤ļ│ĆĒśĢ ņśłņĖĪņŚÉ ņé¼ņÜ®ĒĢśņśĆļŗż. ņØ┤ļŖö ņēśņÜöņåīļź╝ ņØ┤ņÜ®ĒĢ£ ĒĢ┤ņäØņØä ņłśĒ¢ē ĒĢĀ ļĢīļÅä ņ×¼ļŻīņØś ņåīņä▒ ĒŖ╣ņä▒ņØä Ļ│ĀļĀżĒĢśņŚ¼ ņØ┤ņĀä Ļ░ĆņŚ┤ņäĀņØś ņśüĒ¢źņØä ļ░śņśüĒĢśĻ│Āņ×É ĒĢ£ Ļ▓āņØ┤ļŗż. ņāüļ│ĆĒā£ļź╝ ĒżĒĢ©ĒĢśļŖö ņŚ┤ļ│ĆĒśĢļźĀ(ŽĄth+ph)ņØĆ ņĢäļל ņŗØ(2)4)ļź╝ ņé¼ņÜ®ĒĢśņŚ¼ Ļ│äņé░ĒĢĀ ņłś ņ׳ ļŗż. ņØ┤ļĢī ņŚ┤ĒīĮņ░ĮĻ│äņłś(mod) ļśÉĒĢ£ ņāüļ│ĆĒā£ļź╝ Ļ│ĀļĀżĒĢ£ ņŚ┤ĒīĮ ņ░ĮĻ│äņłśņØ┤ļ®░, ņāüļ│ĆĒā£ļź╝ ĒżĒĢ©ĒĢśļŖö ņŚ┤ļ│ĆĒśĢļźĀņØä ļ»ĖļČäĒĢśņŚ¼ ņ¢╗ņØä ņłś ņ׳ļŗż
ņ£ä ņŗØņ£╝ļĪ£ Ļ│äņé░ĒĢ£ ņāüļ│ĆĒā£ļź╝ ĒżĒĢ©ĒĢśļŖö ņŚ┤ļ│ĆĒśĢļźĀņØĆ ņēś ņÜöņåīņØś ņ×¼ļŻī ļ¼╝ņä▒ņ╣śņØĖ ņŚ┤ĒīĮņ░ĮĻ│äņłśļĪ£ ņ×ģļĀźļÉśļ®░ ņēś ņĀłņĀÉņŚÉ ņ×ģļĀźļÉ£ Ļ░Ćņāüņś©ļÅäņÖĆ Ļ│▒ĒĢ┤ņĀĖ ņĄ£ņóģ ļ│ĆĒśĢļźĀļĪ£ ļéśĒāĆļéśĻ▓ī ļÉ£ļŗż. ņØ┤ļĢī Ļ░Ćņāüņś©ļÅäļŖö ņĢäļל ņŗØ(3)4)ņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗż. ņØ┤ļŖö ņŚ┤ņśüĒ¢źļČĆ ĒśĢņāüņŚÉ ļö░ļźĖ ņłśņČĢ ļ│ĆĒśĢĻ│╝ ĻĄĮĒל ļ│ĆĒśĢņØä ļ¬©ļæÉ Ļ│ĀļĀżĒĢ£ ņŗØņØ┤ļŗż.
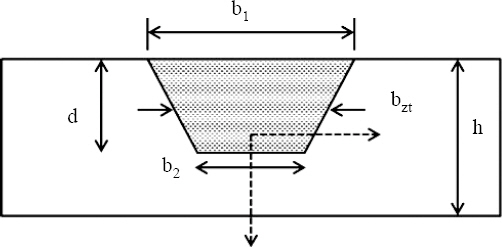
ņ£ä ņŗØņŚÉņä£ b,bzņÖĆ hļŖö Ļ░üĻ░ü ņŚ┤ņśüĒ¢źļČĆņØś ņĄ£ļīĆ ĒÅŁ, ĒīÉņØś Ļ╣ŖņØ┤ņŚÉ ļö░ļźĖ ņŚ┤ņśüĒ¢źļČĆņØś ĒÅŁ ĻĘĖļ”¼Ļ│Ā ĒīÉņØś ļæÉĻ╗śļź╝ ļ£╗ĒĢ£ļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņĀĆĒāäņåīĻ░ĢņØĖ Grade A steelļź╝ ĒĢ┤ņäØņŚÉ ņé¼ņÜ®ĒĢśņśĆļŗż. ņ×¼ļŻīņØś ĒÖöĒĢÖ ņĪ░ņä▒ ņä▒ļČäņ£©ņØĆ Table 1ņŚÉ ņĀĢļ”¼ĒĢśņśĆļŗż.
ņØ╝ļ░śņĀüņ£╝ļĪ£ ņäĀņāüĻ░ĆņŚ┤ņŚÉ ņØśĒĢ┤ Ļ░ĆĻ│ĄļÉśļŖö ņäĀļ░ĢņØś ĒøäĒīÉņØĆ ņāüņś©ņŚÉņä£ ļ▓ĀņØ┤ļéśņØ┤ĒŖĖ(Bainite)ļ¦īņØ┤ ņĪ┤ņ×¼ĒĢśĻ│Ā, ņŚ┤ņøÉņŚÉ ņØśĒĢ£ Ļ░ĆņŚ┤ļŗ©Ļ│äļź╝ Ļ▓¬ņ£╝ļ®░ ņśżņŖżĒģīļéśņØ┤ĒŖĖ(Austenite)ļĪ£ ļ│ĆĒā£ĒĢ£ļŗż. ņØ┤ļĢī ņśżņŖżĒģīļéśņØ┤ĒŖĖļĪ£ ļ│ĆĒā£ĒĢśĻĖ░ ņŗ£ņ×æĒĢśļŖö ņś©ļÅä(Ac1)ļŖö ņĢäļל ņŗØ(4)ļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗż. ņØ┤ ņśżņŖżĒģīļéśņØ┤ĒŖĖļŖö ņłśļāēņŚÉ ņØśĒĢ£ ļāēĻ░üļŗ©Ļ│äļź╝ Ļ▓¬ņ£╝ļ®░ ļ¦łļź┤ĒģÉņé¼ņØ┤ĒŖĖ(Martensite)ļĪ£ ļ│ĆĒā£ĒĢśĻ▓ī ļÉśļŖöļŹ░, ņØ┤ļĢī ņāüļ│ĆĒā£ ņŗ£ņ×æ ņś©ļÅä(Ms)ļŖö ņŗØ(5)ļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗż6,7). Ac1ļŖö ĒīÉņØś ļ│ĆĒśĢļ¤ēņŚÉ ņ¦üņĀæņĀüņ£╝ļĪ£ ņśüĒ¢źņØä ļ»Ėņ╣śļ®░, ĒĢ┤ļŗ╣ ņś©ļÅäļź╝ ņŚ┤ņśüĒ¢źļČĆņØś Ļ▓ĮĻ│äļź╝ ņĀĢņØśĒĢśļŖö ņ×äĻ│äņś©ļÅä(Tc)ļĪ£ ņé¼ņÜ®ĒĢśņśĆļŗż3).
Ļ░ü ņāüļ│ĆĒā£ ņŗ£ņ×æ ņś©ļÅäļź╝ ņØ┤ņÜ®ĒĢśļ®┤ ļāēĻ░üĻ│╝ņĀĢņŚÉņä£ ņś©ļÅäņŚÉ ļö░ļźĖ ņśżņŖżĒģīļéśņØ┤ĒŖĖ(ŽÆ)ņÖĆ ļ¦łļź┤ĒģÉņé¼ņØ┤ĒŖĖ(M)Ļ░ü ņāüļ│ĆĒā£ ņŗ£ņ×æ ņś©ļÅäļź╝ ņØ┤ņÜ®ĒĢśļ®┤ ļāēĻ░üĻ│╝ņĀĢņŚÉņä£ ņś©ļÅä
ņŚÉ ļö░ļźĖ ņśżņŖżĒģīļéśņØ┤ĒŖĖ)ņØś ļČäņ£©ņØä Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗż. ļŗ©, ņ×äĻ│äņś©ļÅä ņØ┤ņāüņØś ņśüņŚŁņØĆ Ļ░ĆņŚ┤ļŗ©Ļ│äņŚÉņä£ ļ¬©ļæÉ ņśżņŖżĒģīļéśņØ┤ĒŖĖļĪ£ ļ│ĆĒā£ĒĢ£ļŗżĻ│Ā Ļ░ĆņĀĢĒĢśņśĆņ£╝ļ®░, ņśżņŖżĒģīļéśņØ┤ĒŖĖ ņŚŁņŗ£ ļāēĻ░üĻ│╝ņĀĢņŚÉņä£ ļ¬©ļæÉ ļ¦łļź┤ĒģÉņé¼ņØ┤ĒŖĖļĪ£ ļ│ĆĒā£ĒĢ£ļŗżĻ│Ā Ļ░ĆņĀĢĒĢśņśĆļŗż8). ļāēĻ░üĻ│╝ņĀĢņŚÉņä£ Ļ░ü ņś©ļÅäņŚÉ ļö░ļźĖ ņśżņŖżĒģīļéśņØ┤ĒŖĖ, ļ¦łļź┤ĒģÉņé¼ņØ┤ĒŖĖ ļČäņ£©ņØĆ ņĢäļל ņŗØ(6)8,9)ņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗż.
ņØ┤ļĢīkļŖö ņāüļ│ĆĒā£ ņåŹļÅäņØ┤ļ®░ Ēāäņåī ĒĢ©ļ¤ēņØ┤ 0.2Wt% ņØ┤ĒĢśņØĖ ņĀĆĒāäņåīĻ░ĢņŚÉņä£ļŖö -0.026ņ£╝ļĪ£ Ļ░ĆņĀĢĒĢĀ ņłś ņ׳ļŗż. ĒŖ╣Ē׳ ņāüļ│ĆĒā£ņŚÉ ņØśĒĢ£ ļČĆĒö╝ ĒīĮņ░ĮņØĆ ļāēĻ░üĻ│╝ņĀĢņŚÉņä£ ņśżņŖżĒģīļéśņØ┤ĒŖĖĻ░Ć ļ¦łļź┤ĒģÉņé¼ņØ┤ĒŖĖļĪ£ ļ│ĆĒā£ĒĢśļŖö Ļ│╝ņĀĢņŚÉņä£ ļ░£ņāØĒĢśļ®░ ļČĆĒö╝ ĒīĮņ░ĮļźĀņØĆ ņĢäļל ņŗØ(7)10)ņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗż.
ņŚ¼ĻĖ░ņä£ XF-P ļŖö ĒÄśļØ╝ņØ┤ĒŖĖ(Ferrite)ņÖĆ ĒÄäļØ╝ņØ┤ĒŖĖ(Pearlite)ņØś ļČäņ£©ņØ┤ļŗż. ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö ņŚ┤ņśüĒ¢źļČĆņŚÉ ņśżņŖżĒģīļéśņØ┤ĒŖĖ ļśÉļŖö ļ¦łļź┤ĒģÉņé¼ņØ┤ĒŖĖļ¦ī ņĪ┤ņ×¼ĒĢ£ļŗżĻ│Ā Ļ░ĆņĀĢĒĢśņśĆņ£╝ļ»ĆļĪ£ XF-Pļź╝ 0ņ£╝ļĪ£ Ļ░ĆņĀĢĒĢ£ļŗż.
ļāēĻ░üĻ│╝ņĀĢņŚÉņä£ ņāüļ│ĆĒā£ ļ│ĆĒśĢļźĀņØĆ ņāüļ│ĆĒā£ņŚÉ ņØśĒĢ£ ļČĆĒö╝ ĒīĮņ░Įņ£╝ļĪ£ ņØĖĒĢ┤ ļ░£ņāØĒĢ£ļŗż. ļĢīļ¼ĖņŚÉ Ļ░ü ņś©ļÅäņŚÉ ļö░ļźĖ ļ¦łļź┤ĒģÉņé¼ņØ┤ĒŖĖņØś ļČäņ£©Ļ│╝ ņśżņŖżĒģīļéśņØ┤ĒŖĖĻ░Ć ļ¦łļź┤ĒģÉņé¼ņØ┤ĒŖĖļĪ£ ļ│ĆĒā£ĒĢśļŖö Ļ│╝ņĀĢņŚÉņä£ ļČĆĒö╝ ĒīĮņ░ĮļźĀņØś Ļ│▒ņ£╝ļĪ£ ļéśĒāĆļé╝ ņłś ņ׳ļŗż. ņØ┤ Ļ░ÆņŚÉ ņŚ┤ĒīĮņ░ĮĻ│äņłśļź╝ ņĀüļČäĒĢ£ ņŚ┤ļ│ĆĒśĢļźĀņØä ļŹöĒĢ┤ņŻ╝ļ®┤ ņŗØ(8)Ļ│╝ Ļ░ÖņØ┤ ņłśņĀĢļÉ£ ņŚ┤ļ│ĆĒśĢļźĀņØä Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗż. ļśÉĒĢ£ Ļ│äņé░ļÉ£ ņŚ┤ļ│ĆĒśĢļźĀņØä ļ»ĖļČäĒĢśļ®┤ ņś©ļÅäņŚÉ ļö░ļźĖ ņŚ┤ĒīĮņ░Į Ļ│äņłśļź╝ Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗż. ņØ┤ļź╝ Fig. 2ņŚÉ ļéśĒāĆļāłļŗż.
ņŚ┤ņśüĒ¢źļČĆļŖö ņ×äĻ│äņś©ļÅä(TC)ņØ┤ņāüņØś ņśüņŚŁņØä ļéśĒāĆļé┤ļ®░ ņØ╝ļ░śņĀüņ£╝ļĪ£ ļ░ś ĒāĆņøÉĒśĢņāüņ£╝ļĪ£ ņĀĢņØśĒĢ£ļŗż. ĒĢśņ¦Ćļ¦ī ĒīÉņØä ņ▓£ņ▓£Ē׳ Ļ╣ŖĻ▓ī Ļ░ĆņŚ┤ĒĢĀņłśļĪØ ņŚŁņé╝Ļ░üĒśĢ Ļ╝┤ļĪ£ ļéśĒāĆļéśļŖö Ļ▓ĮĒ¢źņØ┤ ņ׳ņ¢┤ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņŚ┤ņśüĒ¢źļČĆļź╝ ņé¼ļŗżļ”¼Ļ╝┤ ĒśĢņāüņ£╝ļĪ£ ņĀĢņØśĒĢśņśĆļŗż. ņØ┤ļź╝ Fig. 3ņŚÉ ļéśĒāĆļé┤ņŚłļŗż. ĒīÉņØś Ļ╣ŖņØ┤ņŚÉ ļö░ļźĖ ņŚ┤ņśüĒ¢źļČĆ ĒÅŁņØś Ļ░ÆņØś ņŗØ(9)ņÖĆ Ļ░Öļŗż
ņŗØ(3)Ļ│╝ ņŗØ(9)ļź╝ ņØ┤ņÜ®ĒĢśļ®┤ Ļ░ĆņŚ┤ņŚÉ ņØśĒĢ£ ņ×öļźśļ│ĆĒśĢņØä ļ¬©ņé¼ĒĢĀ ņłś ņ׳ļŖö ļō▒Ļ░ĆņØś Ļ░Ćņāüņś©ļÅäļź╝ Ļ│äņé░ĒĢĀ ņłś ņ׳ļŗż. Fig. 4ņÖĆ Ļ░ÖņØ┤ ņēś ņÜöņåīņØś Ēü¼ĻĖ░ļŖö ņŚ┤ņśüĒ¢źļČĆ ņĄ£ļīĆ ĒÅŁĻ│╝ ļÅÖņØ╝ĒĢśļ®░, Ļ░ĆņŚ┤ņäĀņØ┤ ĒĢśļéśņØĖ Ļ▓ĮņÜ░ Ļ░ĆņŚ┤ņäĀņØ┤ ņ¦ĆļéśĻ░ĆļŖö ņĀłņĀÉņŚÉļ¦ī Ļ│äņé░ĒĢ£ ņāüļČĆ/ĒĢśļČĆ ņś©ļÅäļź╝ ņ×ģļĀźĒĢśĻ│Ā ņØ┤ņÖĖņØś ņĀłņĀÉņŚÉļŖö ņśüņØä ņ×ģļĀźĒĢ┤ņĢ╝ĒĢ£ļŗż. ĒĢśņ¦Ćļ¦ī Ļ░ĆņŚ┤ņäĀņØś Ļ░£ņłśĻ░Ć ņ”ØĻ░ĆĒĢśĻ│Ā, ņä£ļĪ£ Ļ▓╣ņ╣śĻ▓ī ļÉśļ®┤ ĻĘĀņØ╝ĒĢ£ ĒÅŁņØä Ļ░¢ļŖö ņÜöņåīļź╝ ņāØņä▒ĒĢśĻĖ░ ļČłĻ░ĆļŖźĒĢśļŗż. ņØ┤ļ¤¼ĒĢ£ ņØ┤ņ£Ā ļĢīļ¼ĖņŚÉ ļČłĻĘ£ņ╣ÖĒĢśĻ▓ī ļ¦īļōżņ¢┤ņ¦ä ņÜöņåīņØś ņĀłņĀÉņŚÉ ļīĆĒĢ┤ ņČöĻ░ĆņĀüņØĖ Ļ░Ćņāüņś©ļÅä Ļ│äņé░ņØ┤ ĒĢäņÜöĒĢśļŗż. ņØ┤ļŖö ļŗ©ņØ╝ Ļ░ĆņŚ┤ņäĀņŚÉ ņØśĒĢ£ ļ│ĆĒśĢņØä ļ╣äĻĄÉĒĢśņŚ¼ ņēś ņÜöņåīņØś Ēü¼ĻĖ░Ļ░Ć Ļ░Öņ¦Ć ņĢŖņĢäļÅä ņś©ļÅäņןļ¦ī ļÅÖņØ╝ĒĢśĻ▓ī ņĀüņÜ®ĒĢ£ļŗżļ®┤ ļ│ĆĒśĢ Ļ▓░Ļ│╝Ļ░Ć Ļ░ÖļŗżļŖö ņé¼ņŗżņØä ņØ┤ņÜ®ĒĢśņśĆļŗż. ļ©╝ņĀĆ Ļ░ĆņŚ┤ņäĀņØ┤ ņ¦ĆļéśĻ░ĆļŖö ņ×Éļ”¼ņŚÉ ņĀłņĀÉņØ┤ ņ£äņ╣śĒĢśĻ▓ī ĒĢ£ ļÆż, ņØ┤ņÖĖņØś ņÜöņåīļŖö ņ£ĀĒĢ£ņÜöņåī ĒöäļĪ£ĻĘĖļש ļé┤ ņ×ÉļÅÖ ņÜöņåī ĻĖ░ļŖźņØä ņé¼ņÜ®ĒĢśņśĆļŗż. ņØ┤ļĀćĻ▓ī ņāØņä▒ļÉ£ ņĀłņĀÉ ņżæ Ļ░ĆņŚ┤ņäĀņ£╝ļĪ£ļČĆĒä░ Ļ▒░ļ”¼Ļ░Ć ņŚ┤ņśüĒ¢źļČĆ ĒÅŁ ļ│┤ļŗż ņ×æņØĆ ņĀłņĀÉļ¦ī Ļ░ĆļĀżļé┤ņ¢┤ Ļ░ü ņĀłņĀÉņŚÉ ĒĢ┤ļŗ╣ĒĢśļŖö ņś©ļÅäļź╝ Ļ│äņé░ĒĢ£ Ēøä ņĀüņÜ®ĒĢśņśĆļŗż. ņØ┤ Ļ│äņé░Ļ│╝ņĀĢņØĆ Fig. 5ņŚÉ ļéśĒāĆļéśņ׳ņ£╝ļ®░ ņŗØ(10)ņØĆ ņ×äņØśņØś ņĀłņĀÉ(k)ņŚÉ ņĀüņÜ®ĒĢĀ Ļ░Ćņāü ņś©ļÅäļź╝ Ļ│äņé░ĒĢśļŖö ņŗØņØ┤ļŗż.
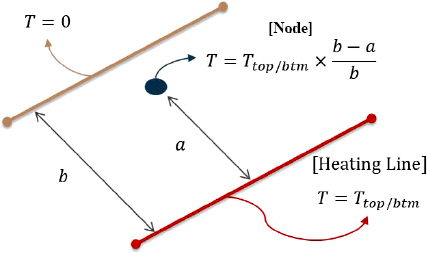
Ļ░ĆņŚ┤ņäĀ ņŻ╝ņ£äņŚÉ ņĀüņÜ®ļÉśļŖö Ļ░Ćņāüņś©ļÅäņןņØ┤ ņäĀĒśĢņĀüņ×äņØä ņØ┤ņÜ®ĒĢśņśĆņ£╝ļ®░bļŖö ņŚ┤ņśüĒ¢źļČĆņØś ĒÅŁ,aļŖö Ļ░ĆņŚ┤ņäĀņ£╝ļĪ£ļČĆĒä░ ņ¦üņäĀĻ▒░ļ”¼ļź╝ ļ£╗ĒĢ£ļŗż. ļśÉĒĢ£ Ļ░ĆņŚ┤ņäĀņØ┤ ĻĄÉņ░©ĒĢśļŖö ņ¦ĆņĀÉņŚÉ ņĪ┤ņ×¼ĒĢśļŖö ņĀłņĀÉņØĆ Ļ░ü Ļ░ĆņŚ┤ņäĀņŚÉ ļīĆĒĢ┤ Ļ│äņé░ĒĢ£ Ļ░Ćņāü ņś©ļÅäļź╝ ņäĀĒśĢņĀüņ£╝ļĪ£ ĒĢ®ĒĢśņŚ¼ ņé¼ņÜ®ĒĢśņśĆļŗż. ĻĘĖļ¤¼ļ»ĆļĪ£ Ļ░ĆņŚ┤ņäĀņØ┤ ļæÉ ļ▓ł ņ¦ĆļéśĻ░ĆļŖö Ļ││ņŚÉ ņ£äņ╣śĒĢ£ ņĀłņĀÉņØĆ ņĄ£ņóģņĀüņ£╝ļĪ£ Ļ░üĻ░ü ņāüļČĆ, ĒĢśļČĆ ņś©ļÅäļĪ£ņŹ© ņŗØ(3) Ļ│äņé░ Ļ▓░Ļ│╝ņØś 2ļ░░ Ļ░ÆņØĖ 2Ttop, 2TbtmņØä ņĀüņÜ®ĒĢśņśĆļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ļæÉ Ļ░Ćņ¦Ć Ļ▓ĮņÜ░ņŚÉ ļīĆĒĢ£ ņŚ┤ ļ│ĆĒśĢ ņśłņĖĪņØä ņłśĒ¢ēĒ¢łļŗż. Ļ░ĆņŚ┤ņäĀ Ļ▓ĮļĪ£ļź╝ Fig. 6ņŚÉ ļéśĒāĆļé┤ņŚłņ£╝ļ®░, ĒīÉņØś Ēü¼ĻĖ░ļŖö ļæÉ Ļ░Ćņ¦Ć Ļ▓ĮņÜ░ ļ¬©ļæÉ ļÅÖņØ╝ĒĢśĻ▓ī650├Ś600├Ś20 mmņØ┤ļ®░, ņŚ┤ņøÉ ļ¬©ļŹĖņØĆ Ļ░ĆņÜ░ņŗ£ņĢł(Gaussian) ņŚ┤ņ£ĀņåŹ(heat flux) ļČäĒżļĪ£ Ļ░ĆņĀĢĒĢśņśĆļŗż. ņĄ£ļīĆ ņŚ┤ņ£ĀņåŹņØĆ 2.5W/mm2, ņŚ┤ņøÉ ļ░śĻ▓ĮņØĆ 30mmņ£╝ļĪ£ Ļ░ĆņĀĢĒĢśņśĆļŗż. ĻĘĖļ”¼Ļ│Ā ņŚ┤ņøÉņØś ņØ┤ļÅÖ ņåŹļÅäļŖö 1.5mm/secļĪ£ Ļ░ĆņĀĢĒĢśņśĆļŗż.
ņåöļ”¼ļō£ ņÜöņåīļź╝ ņØ┤ņÜ®ĒĢ£ ņŚ┤Ēāäņåīņä▒ ĒĢ┤ņäØ Ļ▓░Ļ│╝ņÖĆ ņēś ņÜöņåīļź╝ ņØ┤ņÜ®ĒĢ£ ļ│ĆĒśĢļźĀ Ļ▓ĮĻ│äļ▓ĢņØś ņśłņĖĪ Ļ▓░Ļ│╝ļź╝ 3ņ░©ņøÉ ĒśĢņāüļĪ£ Fig. 7ņŚÉ ļéśĒāĆļāłļŗż. ļśÉĒĢ£ ņśłņĖĪ Ļ▓░Ļ│╝ņØś ņĄ£ļīĆ ļ│ĆĒśĢļ¤ē ņłśņ╣śņÖĆ ĒĢ┤ņäØ ņŗ£Ļ░äņØś ņ░©ņØ┤ļź╝ Table 2ņŚÉ ņĀĢļ”¼ĒĢśņśĆļŗż. ĒĢ┤ņäØņØä ņłśĒ¢ēĒĢ£ ļæÉ Ļ░Ćņ¦Ć Ļ▓ĮņÜ░ ļ¬©ļæÉ 5% ļé┤ņÖĖņØś ņśżņ░©ļź╝ ļ│┤ņśĆļŗż. ĒĢ┤ņäØņŗ£Ļ░äņØĆ ņĢĮ 3,000ļ░░ ļŗ©ņČĢļÉ£ Ļ▓░Ļ│╝ļź╝ ņ¢╗ņØä ņłś ņ׳ņŚłļŗż.
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņŚ┤ļ│ĆĒśĢļźĀ ĻĖ░ļ░śņØś ļ│ĆĒśĢļźĀ Ļ▓ĮĻ│äļ▓ĢņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņäĀņāüĻ░ĆņŚ┤ņŚÉ ņØśĒĢ£ ĒøäĒīÉņØś ļ│ĆĒśĢņØä ņśłņĖĪĒĢśņśĆļŗż. ņ£ĀĒĢ£ņÜöņåī ĒĢ┤ņäØņØä ļŗ©ņł£ĒÖöĒĢśļŖö Ļ│╝ņĀĢņŚÉņä£ ņśłņĖĪ ņĀĢĒÖĢļÅäļź╝ ļåÆņØ┤ĻĖ░ ņ£äĒĢ┤ ņāüļ│ĆĒā£ļź╝ ĒżĒĢ©ĒĢśļŖö ņŚ┤ļ│ĆĒśĢļźĀņØä ņé¼ņÜ®ĒĢśņśĆņ£╝ļ®░, ņ×¼ļŻī ņä▒ļČäņØś ļö░ļźĖ ņ░©ņØ┤ļź╝ ļ│ĆĒśĢ ņśłņĖĪņŚÉ ļ░śņśüĒĢśņśĆļŗż. Ļ░ĆņŚ┤ņäĀņØä ņżæņŗ¼ņ£╝ļĪ£ ļ╣äĻĘĀņØ╝ ņÜöņåīņŚÉ Ļ░Ćņāü ņś©ļÅäņןņØä ļČĆņŚ¼ĒĢśņŚ¼ ļō▒Ļ░Ć ņŚ┤ĒĢśņżæņØä ļ░śņśüĒĢśņśĆļŗż. 3ņ░©ņøÉ ņŚ┤Ēāäņåīņä▒ ļ│ĆĒśĢ ĒĢ┤ņäØĻ│╝ ļ│ĆĒśĢļźĀ Ļ▓ĮĻ│äļ▓ĢņØä ņØ┤ņÜ®ĒĢ£ ļ│ĆĒśĢ ņśłņĖĪ Ļ▓░Ļ│╝ņŚÉņä£ ņĄ£ļīĆ ļ│ĆĒśĢļ¤ēĻ│╝ ĒĢ┤ņäØņŗ£Ļ░äņØä ļ╣äĻĄÉĒĢ©ņ£╝ļĪ£ņŹ© ņŚ┤ļ│ĆĒśĢļźĀ ĻĖ░ļ░śņØś ļ│ĆĒśĢļźĀ Ļ▓ĮĻ│äļ▓ĢņØ┤ 3ņ░©ņøÉ ņŚ┤Ēāäņåīņä▒ ĒĢ┤ņäØņŚÉ ĻĘ╝ņĀæĒĢśļŖö ņĀĢĒÖĢĒĢ£ ņśłņĖĪņØ┤ Ļ░ĆļŖźĒĢśļ®░, ņśłņĖĪ ņŗ£Ļ░äņØ┤ ņŗĀņåŹĒĢ©ņØä Ļ▓Ćņ”ØĒĢśņśĆļŗż. ņČöĒøäņŚÉ ņŗżņĀ£ ņŗżĒŚśņØä ĒåĄĒĢ┤ ņśłņĖĪ ļ░®ļ▓ĢņØä ņĀüņÜ®ĒĢśĻ│Ā ļ╣äĻĄÉĒĢśļŖö ņŚ░ĻĄ¼ļź╝ ņ¦äĒ¢ēĒĢĀ ņśłņĀĢņØ┤ļŗż.
Ēøä ĻĖ░
ņØ┤ ņŚ░ĻĄ¼ļŖö KIAT ņ¦ĆņøÉņØś 2018ļģä ņĪ░ņäĀĒĢ┤ņ¢æņé░ņŚģ Ēć┤ņ¦üņØĖļĀźĒÖ£ņÜ® ņĀäļ¼ĖņØĖļĀźņ¢æņä▒ņé¼ņŚģ (Ļ│╝ņĀ£ļ▓łĒśĖ: N0002361), ņé░ņŚģĒåĄņāüņ×ÉņøÉļČĆ ļ░Å ĒĢ£ĻĄŁņé░ņŚģĻĖ░ņłĀĒÅēĻ░ĆĻ┤Ćļ”¼ņøÉ(KEIT) ņŚ░ĻĄ¼ļ╣ä ņ¦ĆņøÉņŚÉ ņØśĒĢ£ ņŚ░ĻĄ¼ņ×ä (Ļ│╝ņĀ£ļ▓łĒśĖ: 10077588)
References
1. Chang Doo. Jang, A study on the prediction of deformations of plates due to line heating using a simplified thermal elasto-plastic analysis, Journal of Ship Production. 13(1) (1997) 22ŌĆō27.
[CROSSREF] [PDF]
[CROSSREF] [PDF]
2. Chang Doo. Jang, Yun Sok. Ha, and Dae Eun. Ko, An Improved Inherent Strain Analysis for the Prediction of Plate Deformations Induced by Line Heating Considering Phase Transformation of Steel, The Thirteenth International Offshore and Polar Engineering Conference. (2003)
3. Yunsok. Ha, Jinhyuk. Yang, Seokhee. Won, and Myungsu. Yi, Development of Thermal Distortion Analysis Method Based on Inherent Strain for TMCP Steels, International Journal of Precision Engineering and Manufacturing. 26(3) (2008) 61ŌĆō66. https://doi.org/10.3744/SNAK.2008.45.1.93
[CROSSREF]
[CROSSREF]
4. Chang Doo. Jang, Yun Sok. Ha, Dae Eun. Ko, and Sung Choon. Moon, Determination of Inherent Strain Regions to Estimate Plate Deformation by Line Heating, Journal of the Society of Naval Architects of Korea. 39(1) (2002) 82ŌĆō89. https://doi.org/10.3744/SNAK.2002.39.1.082
[CROSSREF] [PDF]
[CROSSREF] [PDF]
5. Yunsok. Ha, A Study on Weldment Boundary Condition for Elasto-Plastic Thermal Distortion Analysis of Large Welded Structures, Journal of KWJS. 29(4) (2011) 48ŌĆō53. https://doi.org/10.5781/KWJS.2011.29.4.410
[CROSSREF]
[CROSSREF]
6. P. Payson and C.H. Savage, Martensite Reactions in Alloy Steels, Transactions ASM. 33 (1944) 261ŌĆō275.
7. K. W. Andrews, Empirical formulae for the calculation of some transformation temperatures, J. Iron Steel Inst. (1965) 721ŌĆō727.
8. G. Krauss and A. R. Marder, The morphology of martensite in iron alloys, Metallurgical Transactions. 2(9) (1971) 2343
[CROSSREF]
[CROSSREF]
9. D. Koistinen and R. Marburger, A General Equation Pre-scribing the Extent of the Austenite-Martensite Trans-formation in Pure Iron-Carbon Alloys and Plain Carbon Steels, Acta Metallurgica. 7 (1959) 59ŌĆō60. https://doi.org/10.1016/0001-6160(59)90170-1
[CROSSREF]
[CROSSREF]
10. E. C. Bain and H. W. Paxton, Alloying Elements in Steel, American Society for Metals. (1966)
11. Yunsok. Ha, Analytical methodology obtaining an optimal welding sequence for least distortion of welded structure. Analysis, Journal of KWJS. 31(3) (2013) 54ŌĆō59. https://doi.org/10.5781/KWJS.2013.31.3.54
[CROSSREF]
[CROSSREF]
-
METRICS

-
- 14 Crossref
- 4,317 View
- 87 Download
- ORCID iDs
-
Jeeyeon Heo

https://orcid.org/0000-0002-1820-5368Jang-Hyun Lee

https://orcid.org/0000-0002-7164-1732 - Related articles




 PDF Links
PDF Links PubReader
PubReader ePub Link
ePub Link Full text via DOI
Full text via DOI Download Citation
Download Citation Print
Print